Rectangle – Definition & Area of Rectangle

A rectangle is a geometric form with four parallel and opposing sides. The area of a rectangle is defined as the number of unit squares that it can accommodate. The area of a rectangle may alternatively be defined as the region occupied by the rectangle’s perimeter. You may notice that the tiles in your house are rectangular in shape. As a result, the formula for calculating the area of the tile is length multiplied by breadth, or l * b, where we use the letter l to denote the length and b to denote the breadth of a rectangle. The resulting value is always expressed in square units.

The rectangle’s length is defined as the longest as well as the horizontal side, but the width is defined as the vertical line that is shorter than the length. In this post, we will attempt to discuss some fundamental components of the area of a rectangle, such as area calculations, perimeter, and so on.

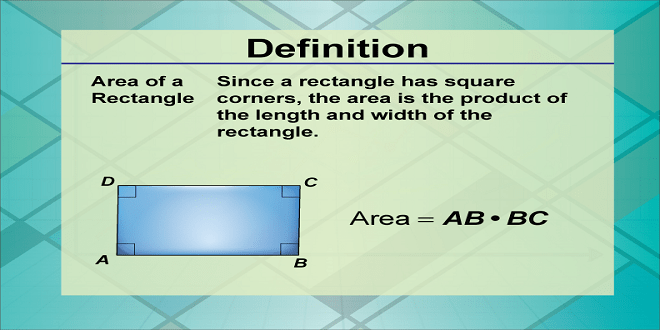
What is the Area of a Rectangle?

The area covered by a 2-dimensional form in a plane is referred to as its area. It is expressed in square units. As a result, the area of any given rectangle equals the region bounded by its outside edges. It is equivalent to the product of length and breadth. So the area of rectangle formula is:

Properties of Rectangle

The features of a rectangle allow us to recognize the figure at a glance. A rectangle is a two-dimensional geometric shape with 4 sides, 4 vertices, & 4 angles. Let’s go through the few important properties of a rectangle-

• It has four vertices and four sides.
• Every vertex of a rectangle has a 90-degree angle.
• The opposing sides are parallel and equal.
• Each other’s diagonals are bisected.
• The perimeter of a circle is equal to twice the sum of its length as well as width.
• It has four right angles and is a parallelogram.
• 360 degrees is the sum of all interior angles of any given rectangle.

Some examples based on the Area of Rectangle

As previously stated, the area of a rectangle may be measured or estimated by multiplying its breadth by its length. The following are some instances of rectangular areas:

Example 1) A rectangle’s length and breadth are 11 m and 7 m respectively. What is the area?

Solution) Let’s note the information given in the question,

The length of the given rectangle is 11 m

The breadth of the given rectangle is 7 m

Using the formula of area of rectangle discussed above = breadth of the rectangle * length of the rectangle

11 metre * 7 metre  = 77 metre square units.

Therefore, the area of the rectangle is equivalent to 60 metre square units.

Example 2) The rectangular playground next to your house has a length of 5 cm and a breadth of 4 cm. Find the area of the given playground?

Solution) Let’s note the information given in the question,

The length of the given rectangular playground is 5 cm

The breadth of the given rectangular playground is 4 cm

Using the formula of area of rectangle discussed above = breadth of the rectangular playground * length of the rectangular playground

5 cm * 4 cm  = 20 cm square units.

Therefore, the area of the rectangle is equivalent to 20 cm square units.

Rectangles in Daily Life

Have you ever wondered if you are surrounded by shapes? The book you read, the table you place your laptop on, mousepads, the 10 rupees note, the phones you use, the television screen you watch all are in the shapes of a rectangle.